<reference>
Fei Tony Liu, Kai Ming Ting, Zhi-Hua Zhou, Isolation Forest
해당 글은 Isolation Forest 논문 내용 요약 및 구현, 관련 의견을 정리하였음. (구현 : python3)
논문 요약
1. Introduction
기존 모델 기반(model-based) 이상 탐지 방법들은 정상치(normal instances)에 대한 프로필을 생성하고, 이와 일맥하지 않는 대상을 이상치로 분류하는 방식이다. 필자에 따르면, 이러한 접근 방식은 이상치가 아닌 정상치 프로필(profile)에 적합화(optimized)되기 때문에 오히려 이상치 탐지 자체는 부정확하고, 더 나아가 높은 연산 복잡도로 인해 고차원 데이터에 적용하기 어렵게 만든다. 따라서 필자는 기존 방법과 달리, 이상치를 고립(isolate)시키는 방법을 제안한다.
이를 위해, 이상치는 1) 상대적으로 적으며, 2) 정상치와는 다른 속성값을 갖는다는 양적 특성을 활용해야 한다. 즉, 이상치란 양적으로 적고 다르며(few and different), 이러한 특성이 이상치를 쉽게 고립될 수 있게 한다. 이로 인해 트리 구조(tree)를 사용하여 모든 데이터를 고립시키게 되면, 이상치는 루트 노드에 가깝게 위치한다. 이러한 트리 구조의 고립 특성(isolation characteristic)이 이상치를 탐지하는 본 방법의 핵심이며, 이에 착안하여 해당 방법을 Isolation Forest라고 명명하였다.
* 여기서 말하는 트리 구조에서의 '고립'이란, 조금 더 구체적으로 말하면 데이터를 단말 노드까지 배치시키는 것을 의미한다.
* 햇갈리지 말아야 할 것은, 이상치만 고립된다는게 아니다. 트리를 통해 정상/이상치 모두를 고립시켰을 때, 이상치는 그 특성으로 인해 빠르게(쉽게) 고립된다는 말이다.
Isolation Forest, 또는 iForest는 주어진 데이터의 Isolation Tree(iTree) 앙상블(ensemble)로 이뤄지며, 이상치는 각 iTree에서 짧은 평균 "path length"를 갖는 데이터(instance)을 의미한다. 필자에 따르면 이 방법은 1) iTree의 수, 2) 샘플(sub sample)의 크기 정도만 변수로 설정하면 되며, 많은 수의 iTree와 샘플을 요구하지 않기 때문에 굉장히 빠른 속도로 이상치를 탐지할 수 있다.
2. Isolation and Isolation Tree
본고에서의 '고립'이란, '한 개의 인스턴스를 나머지 인스턴스로 부터 분리하는 것'을 의미한다. 언급했듯 이상치의 특성으로 인해 이상치는 쉽게(=상대적으로 빠르게) 고립된다. 이 방법에서는 이상치 뿐 아니라 모든 인스턴스들이 고립될 때까지 임의적, 재귀적으로 인스턴스를 분리하는 작업을 수행한다. 이러한 방식은 이상치에 대하여 상대적으로 적은 분리 작업이 필요하며(= 짧은 path lenght), 독특한 속성을 갖는 인스턴스일수록 초기 분할 작업에서 고립될 가능성이 높다.
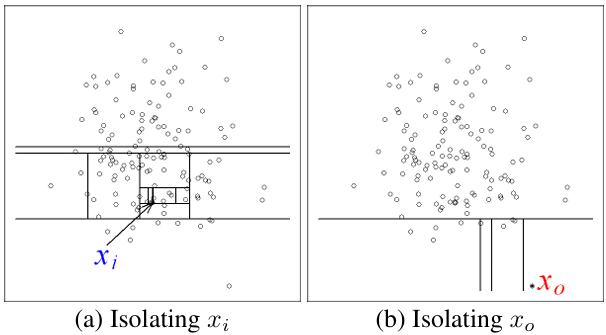
'임의로 분할(random partitioning)하였을 때, 이상치일 수록 빠르게 고립된다.'는 아이디어는 위의 예시를 통해 확인할 수 있다. 위 예시를 설명하기 앞서 임의적, 재귀적으로 데이터를 고립시키는 방법을 간략히 설명하면 다음과 같다.
우선, N차원의 데이터 M개가 존재한다고 가정한다. 이후 (1) N차원 중 임의의 속성(차원)을 선택하고, (2) 해당 속성(차원)의 값 중에서 최대 ~ 최소 사이의 임의값을 선택한다. (3) 이후 선택한 임의의 값을 기준으로 M개의 데이터를 양분한다. 위 그림의 직선은 이러한 방식으로 데이터를 양분했을 때 생성된 것이며, 각 직사각형 모형 내에 데이터가 1개만 존재할 때까지 위 과정을 반복한다. 위 그림은 각 데이터 $x_{i}$, $x_{0}$가 고립될 때까지 필요한 분할이 얼만큼인지를 보여준 예시라고 생각하면 된다.
위 그림을 보면 정상치인 $x_{i}$를 고립시킬 때 보다 이상치인 $x_{0}$를 고립시킬 때, 훨씬 적은 개수의 '분할 직선(partition)'필요한 것을 볼 수 있다. 이러한 재귀적 분할(recursive paritioning)은 트리 구조로 치환하여 표현할 수 있으며, 고립됐다는 것은 해당 데이터가 단말 노드에 위치한 것으로 바꿔 이해할 수 있다. 따라서 특정 데이터를 고립시키기 위해 필요한 분할 직선(partition)의 수는 곧 루트노드에서 해당 단말 노드까지 가는데 필요한 엣지의 수(=path length)와 동일하다.
* 위에서 제시한 방법은, 다차원의 데이터를 트리에 저장할 때 사용하는 일반적인 방법이다. (특정 기준으로 차원을 선택하고, 그 차원 내부에서 특정 기준으로 값을 선택하여 데이터를 양분하는 방법)
다만, 분할하고자 하는 차원과 값을 임의로 선택하기 때문에, 매번 트리를 생성할 때마다 특정 데이터에 대한 path length의 수는 다를 수 있다. 따라서 필자는 여러 트리를 생성하여 path length의 평균을 구하고 이를 'path length 기댓값'으로 가정한다. 아래의 그림을 보면, $x_{0}$, $x_{1}$ 의 평균 path length는 트리의 수를 증가시킬수록 특정 지점에 수렴하는 것을 볼 수 있다. 본 논문에서는 1,000개의 트리를 사용하였고, $x_{0}$, $x_{1}$의 평균 path length는 각각 4.02, 12.82에 수렴하였다.

Definition : Isolation Tree
Isolation Tree는 다음과 같이 정의(생성)된다. (이미 위에서 제시한 방법과 동일하다.) 우선 $T$ 를 Isolation Tree의 노드라고 하면, $T$는 단말 노드이거나, 두 개의 자식노드 $T_{l}$, $T_{r}$ 를 모두 갖고 있는 노드여야 한다(=proper binary tree). 이때 $T_{l}$, $T_{r}$ 은, 어떠한 속성(차원) $q$ 와 해당 차원에 속하는 "split value" $p$ 를 선택한 후, 해당 차원에서 $p$보다 작은 값을 갖은 데이터는 $T_{l}$, 큰 값은 $T_{r}$로 양분된 노드라고 생각하면 된다. 이를 재귀적으로 수행하면 Isolation tree가 생성되며, 데이터의 수가 n개일 때, 단말 노드의 수는 n, 비단말 노드는 (n-1)이 된다. 따라서, 트리의 총 노드 수는 2n-1이다.
이때, 단말 노드로 분류되는 기준은 (1) 트리가 "높이 제한"에 도달하였거나, (2) 양분하고 남은 노드의 수가 1이거나, (3) 양분 시 남아있는 데이터가 모두 같은 경우이다. 이상 탐지의 목표는 이상치의 정도를 반영한 랭킹을 제공하는 것이다. 따라서 이상치를 탐지하는 한 가지 방법은 해당 데이터의 path length 또는 이상치 점수(anomaly score)에 따라 데이터를 정렬하는 것이다. 이때 이상치는 리스트의 맨 위에 위치하게 된다.
Definition : Path Length
데이터 x에 대한 $h(x)$ 는 루트 노드에서 해당 데이터(단말 노드)에 도달하기 까지 거쳐간 엣지의 수로 측정되는 값이다. 본고의 저자는 이 $h(x)$의 값을 측정하기 위하여, 해당 데이터가 이진 트리구조라는 점에 착안한다. 즉, $h(x)$도 이진 트리에서 특정 x에 도달하기까지의 길이를 측정한 것이므로, 이는 이진트리의 unsucessful search와 동일하다. 이때 unsucessful search의 평균 path length는 다음과 같다.
$c(n) = 2H(n-1) - 2(n-1)/n$
여기서 $H(i)$는 조화수(harmonic number)이며, 이는 $ln(i) + 0.5772156649$ (오일러상수)로 근사할 수 있다. 따라서 이를 근사값으로 다시 정리하면 다음과 같다.
$c(n) = 2 * (ln(n-1) + 0.5772156649) - 2(n-1)/2$
즉, $c(n)$은 n이 주어졌을 때, $h(x)$의 평균이므로, 이를 이용하여 $h(x)$를 정규화(normalize)할 수 있다. 따라서 이 점을 활용하여 다음과 같이 데이터 x에 대한 이상치 점수(anomaly score) $s는$ 다음과 같이 정의된다. $E(h(x))$는 각 트리의 $h(x)$의 평균값을 의미한다.
$s(x,n) = \frac{-E(h(x))}{c(n)}$
위의 anomaly score 점수는 다음과 같이 3가지 케이스로 나눠볼 수 있으며 그 의미는 다음과 같이 해석할 수 있다.
1) $E(h(x)) \rightarrow c(n)$이면, $s \rightarrow 0.5$가 된다.
> $h(x)$의 평균값이 $c(n)$에 수렴하므로, 이는 해당 데이터가 갖는 path length가 정상치의 범위에 들어있음을 의미한다. 만일 모든 데이터의 $s$값이 모두 0.5 근처로 계산된다면, 해당 데이터 셋 내에는 이상치가 없는 것으로 간주할 수 있다.
2) $E(h(x)) \rightarrow 0$이면, $s \rightarrow 1$이 된다.
> $h(x)$의 평균값이 0, 즉 매우 작은 상황으로, 이는 의심할 여지없이 이상치로 간주할 수 있다.
3) $E(h(x)) \rightarrow n-1$이면, $s \rightarrow 0$이 된다.
> $h(x)$의 평균값이 데이터의 수에 따라 점차 선형적으로 증가하고 있으므로, 이는 이상치와는 완전히 벗어난 '안전한' 정상치라고 볼 수 있다.
여기서 $s$는 $h(x)$에 대한 단조함수이며, 위에서 설명한 $s$와 $h(x)$의 관계는 아래의 그림에서 확인할 수 있다. 다만, 다음과 같은 조건이 전제되어 있다. $0 < h(x) <= n-1$에 대하여 $0 < s < 1$이다.
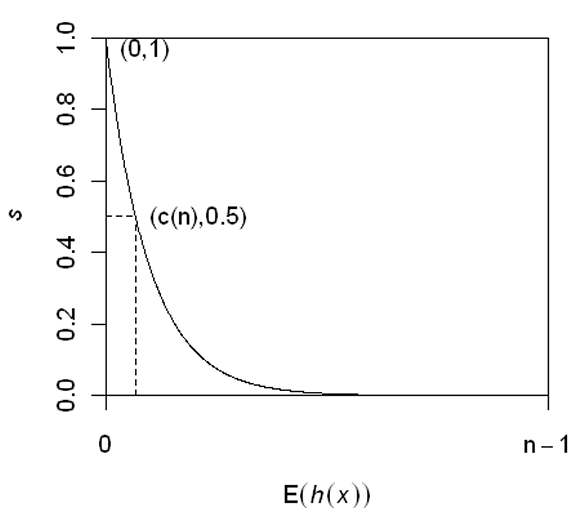
* 다만, 실제 데이터에 대하여 anomaly score를 계산하면 반드시 1에 가까운 수치로 이상치가 나오거나, 역으로 0 또는 0.5에 가까울 때만 정상치를 의미하는 것은 아니다. anomaly score는 상대적인 값이며, 따라서 이를 다른 데이터의 score와 비교하는 방식으로 해석해야 한다.
3. Characteristic of Isolation Trees
본 장에서는 iTree의 특성과 iTree가 swamping과 masking을 다루는 방식을 설명한다. 여기서 swamping이란 정상치를 이상치로 분류하는 것을 의미하며, Masking이란 이상치가 지나치게 많이 존재하여 이상치 식별이 불가능한 경우를 의미한다(concealing their own presence). 저자에 따르면 iForest가 학습 데이터의 다수를 차지하는 정상치를 모두 고립시켜야만 하는 것은 아니기 때문에, 모든 정상치를 고립시켜 모델을 생성하는 것 없이, 적은 양의 샘플 데이터만을 이용하여 '부분 모델'을 만드는것 만으로도 충분히 잘 작동한다.
일반적으로 swamping은 정상치가 이상치에 매우 근접하게 위치한 경우 발생하기 쉬우며, 이 경우 이상치를 정상치와 분리하기 위하여 많은 수의 parition들이 필요(=루트로 부터 path length가 길어짐)하기 때문에, 막상 정상치와 구분하는 것이 어려워질 수 있다. masking의 경우도, 이상치의 군집이 지나치게 크고 넓은 경우 발생하게 되는데, 이 경우도 이상치를 분리하기 위하여 지나치게 많은 partition이 필요하게 된다. 이러한 상황에서는 이상치 탐색이 오히려 더 어려워질 수밖에 없다. 여기서 주목할 점은 swamping, masking은 이상치 탐지를 수행하기에 지나치게 많은 데이터 주어졌기 때문에 발생하는 현상이라는 점이다.
흥미로운 점은 위에서 언급한 isolation의 특성(샘플 데이터를 통해 부분 모델을 만들어도 충분히 잘 작동한다.)이 swamping, masking 효과를 즉각적으로 완화시켜 줄 수 있다는 점이다. 이는 (1) 샘플링을 통해 데이터의 사이즈를 조절할 수 있고, (2) 이러한 방식으로 만들어진 isolation tree는 각 샘플이 가지고 있는 이상치와 정상치의 서로 다른 특성을 반영할 수 있기 때문이다. 이러한 효과는 아래의 그림 예시를 통해 설명할 수 있다.
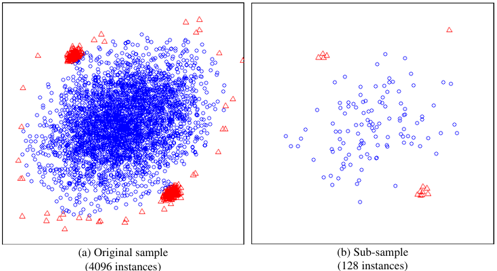
위 그림의 (a)를 보면 중심에 위치한 정상치 군집을 기준으로 상,하에 이상치 군집이 높은 밀도로 정상치 가까이 생성되어 있는 것을 볼 수 있다. 이 데이터 셋에 대하여 샘플링을 수행한 그림(b)를 보면, 이상치가 정상치와 확연하게 구분되는 것을 볼 수 있다. 이상치와 근접해있던 정상치가 모두 제거되었고, 이상치의 군집 정도와 수량이 현격히 줄어들어 보다 효과적으로 식별할 수 있다. 따라서 본고의 필자에 따르면, 샘플링을 통해 iForest에서는 swamping, masking 영향을 효과적으로 다룰 수 있다.
4. Anomaly Detection using iForest
*기존 논문에서는 각 단계를 의사코드로만 설명하지만, 본 글에서는 의사코드와 함께 실제 구현하는 방법을 함께 다룬다.
iForest를 이용한 이상탐지 모델은 2단계로 구성된다. 첫 단계는, 샘플링을 통해 isolation tree를 생성하는 것이다. 두 번째 단계는 테스트 인스턴스를 iTree에 대입하여 각 인스턴스에 대한 anomaly score를 계산하는 단계다.
4.1 Training Stage
이 단계는 위에서 설명한 바와 같이, 데이터 샘플을 통해 iTree를 생성하는 단계다. iTree는 위에서 설명한 바와 같이 각 데이터에 대하여 '임의적, 재귀적' 방법으로 생성하면 된다. 이때 트리의 높이 제한(l)은, 샘플 데이터의 수를 n이라고 했을 때, $l = ceiling(log_{2}n)$으로 하며, 이는 트리의 평균 높이에 근사한 수치다. 트리의 높이를 평균 높이로 제한하는 이유는 현재 우리의 주된 관심은 평균 높이보다 짧은 길이를 갖는 이상치에 있기 때문이다.
* 즉, 우리의 관심은 짧은 높이를 갖는 이상치에 있으므로, 특정 높이 이상으로 깊어지는 데이터는 적당히 고립시키는 편이 계산 측면에서도 효율적이다.
iTree와 iForest를 만드는 의사코드는 다음과 같다.


<Algorithm 1>은 iForest 의사코드로, 트리의 높이($l)를 설정한 후, 여러 트리를 만들고 이를 합치는 방식(=Forest)으로 작성되어있다. <Alogirthm 2>는 iTree를 생성하는 과정을 설명하고 있는데, 어쨌든 트리 구조이기 때문에 노드를 생성하는 과정이 필요하다. 논문에서는 노드를 어떤 방식으로 구현할지 개별적인 언급이 없으므로, 본고에서는 노드 구현부터 진행한다. 노드는 다양한 방법으로 생성할 수 있으나, 여기서는 노드 객체(class)를 생성하는 방법으로 진행한다. 여기서 노드는 다차원 데이터를 담을 수 있는 노드여야 하므로 다음과 같이 구현할 수 있다.
* 위에서도 언급한 바와 같이, 다차원 데이터를 담는 (이진)트리구조는 데이터를 분할할 때 특정 차원과 해당 차원의 특정값을 기준으로 나누는 방식이 일반적(위 논문에서만 취하는 특이한 방법은 아니다)이다. 여기서도 이와 동일한 방법을 취하고 있다. 따라서 해당 차원과 값을 담을 수 있는 변수가 필요하다. 그냥 이러한 노드 구조가 일반적이라는 말이 하고 싶었음. (예 - SIFT에서 디스크립터 매칭시 사용되는 BBS 알고리즘 등)
# 다차원 데이터를 담을 수 있는 노드 구조
import numpy as np
class MultiNode:
def __init__(self,
value : np.ndarray,
sDim : int,
sVal,
left = None,
right = None):
"""
(2차원 이상인) 다차원 데이터에 대한 노드
예)
x1 = [1, 2, 3, 4, 5]
x2 = [4, 5, 2, 1, 3]
...
:param value: 해당 노드의 값 (x) > A x B일 수 있음 (A>=1)
:param sDim: 분할의 기준이 되는 차원의 수 (dtype : int)
:param sVal: 분할의 기준이 되는 차원 내 값
:param left: 분할 차원 내 value를 기준으로 해당 노드의 좌측에 위치하는 노드의 링크
:param right: 분할 차원 내 value를 기준으로 해당 노드의 우측에 위치하는 노드의 링크
ㄴ 단말노드의 경우, left, right가 None이 될 수 있으므로 기본값을 default로 설정
"""
self.value = value
self.sDim = sDim
self.sVal = sVal
self.left = left
self.right = right
위 노드를 기준으로 iTree를 생성하는 로직은 다음과 같다. 해당 코드의 핵심은 입력된 데이터를 단말노드로 간주할 것인지를 판단하는 것으로, 논문 내용에 따르면 단말노드로 간주할 수 있는 경우는 크게 3가지다.
(1) 트리가 "높이 제한"에 도달하였거나,
(2) 양분하고 남은 노드의 수가 1이거나,
(3) 양분 시 남아있는 데이터가 모두 같은 경우
이 3가지 조건 중 어느 것에도 해당되지 않으면, 1) 분할의 기준이 되는 차원(속성)을 임의로 선택, 2) 해당 차원 내 분할의 기준이 될 값을 임의로 선택, 3) 해당 값을 기준으로 데이터를 좌, 우로 분할하는 세 단계를 재귀적으로 수행하며, 재귀를 수행할 때마다 노드의 높이(hl, height limit)는 1씩 증가한다.
def iTree(x : np.ndarray,
hl : int,
ch = 0):
"""
<Algorithm 2>
입력받은 데이터 x에 대하여, isolation tree를 생성한다.
:param x: 입력받은 2차원 배열 데이터
예)shape of x : N x D (N : 데이터의 수, M : 데이터의 차원)
:param ch: 현 노드의 높이 (current height)
:param hl: 트리의 높이 제한 (height limit)
:return: iTree
"""
# STEP 1: 단말 노드에 해당하는지 확인
"""
<단말 노드에 해당할 조건>
1) 입력받은 데이터의 수가 1개다.
2) 조건 1)을 만족하지는 않지만, 입력받은 데이터가 서로 모두 같다.
3) 해당 데이터의 높이가 트리의 높이 제한에 도달하였다.
"""
# 단말 노드에 해당하는 경우
if x.shape[0] == 1 or ch >= hl or (x[0]==x).all():
return MultiNode(value=x,
sDim=None,
sVal=None)
# 단말 노드에 해당하지 않는 경우
else:
sDim = np.random.choice(x.shape[1]) # 분할 차원 임의 선택
sVal = (np.max(x[:, sDim])-np.min(x[:, sDim]))*np.random.random() + np.min(x[:, sDim]) # 분할 값 임의 설정
mask = x[:,sDim] < sVal
return MultiNode(value=x,
sDim=sDim,
sVal=sVal,
left=iTree(x=x[mask], ch=ch+1, hl=hl),
right=iTree(x=x[~mask], ch=ch+1,hl=hl))
이제 이 트리들의 집합으로 iForest를 생성하면 된다. iForest 자체는 iTree의 합집합이기 때문에 어려울 것이 없다. 다만, 트리의 높이 제한을 설정해야하는데, 위에서 언급한 바와 같이 입력받는 샘플 사이즈에 밑이 2인 로그를 취한다. 다시 한 번 말하지만, 트리의 높이를 평균으로 제한하는 이유는, 현재 목표가 평균 노드 길이 보다 짧은 값(이상치)를 찾아내는 것이므로, 평균 높이에 도달한 데이터는 정상치로 간주해버리는 것이 연산 차원에서 효율적이기 때문이다.
def iForest(self,
x : np.ndarray,
n : int,
s : int):
"""
<Algorithm1>
입력받은 데이터 x에 대하여, iForest를 생성한다.
:param x: 입력받은 2차원 배열 데이터
예) x = N x D (N : 데이터의 수, M : 데이터의 차원)
:param n: 트리의 수
:param s: 샘플 사이즈의 크기 (sub sample size)
:return: iForest
"""
# initialize iForest
iForest = []
hl = np.ceil(np.log2(s)) # 트리의 높이 제한 (평균 높이로 제한)
for _ in range(n):
sub = np.random.choice(x.shape[0], s, replace=False) # 비복원추출
subTree = iTree(x=x[sub], hl=hl, ch=0)
iForest.append(subTree)
return iForest
저자에 따르면 각 변수의 기본값은 트리의 수는 100, 데이터의 샘플 크기는 256 정도로 시작하는 것이 적당하며, 특히 데이터 샘플 크기의 경우 지나치게 늘리게 되면 데이터 처리 시간만 오래 걸릴 뿐 성능 자체는 크게 개선되지 않는다고 한다.
4.2 Evaluating Stage
4.1 Traning stage를 통해 iForest 모델 생성을 완료했다면, 이제 특정 데이터에 대한 anomaly score, $s$를 계산할 수 있다. $s$는 $E(h(x))$로 표현할 수 있는데, $h(x)$의 평균값을 의미하며, $h(x)$는 iForest를 구성하고 있는 각 iTree에 $s$를 구하고자하는 데이터 x를 넣었을 때, 단말노드에 도달하기까지 통과하는 엣지의 수(=$e$)를 의미한다. 다만, 단말노드에 도달했을 때, 단말노드의 데이터 수가 1개를 초과할 수 있다. 이는 위에서 언급한 단말노드의 생성 조건 때문이다. 이 경우, 남아있는 데이터의 수를 $Size$라고 했을 때, 엣지의 수인 $h(x)$는 $e + c(Size)$로 계산한다. 여기서 $c$는 위에서 언급한 $c(n) = 2H(n-1) - 2(n-1)/n$이다. 이는 데이터 수가 1이 아닐 때, 데이터 수에 대한 평균 기댓값으로 $e$를 보간하는 것이라고 생각하면 된다.
먼저 unsuccessful search의 평균값을 계산할 수 있는 c와 이를 이용하여 입력 x에 대한 탐색거리를 계산하는 pathLength 함수를 구현한다.
def c(self, n):
"""
Unsuccessful search의 평균값
:param n: 노드의 수
:return: avg. of unsuccessful search
"""
return 2.*(np.log(n-1) + np.euler_gamma) - 2*(n-1)/2.
def pathLength(x : np.ndarray,
t : MultiNode,
pl : int):
"""
:param x: path length를 계산할 데이터 x (shape of x : 1 x D)
:param t: iTree
:param pl: current path length
:return:
"""
# 단말 노드에 도달한 경우 (proper binary tree이므로, 한쪽이라도 자식이 없으면 단말노드다.)
if t.left is None:
return pl + c(t.Val.shape[0])
else:
if x[t.sDim] < t.sVal:
return pathLength(x, t.left, pl+1)
elif x[t.sDim] >= t.sVal:
return pathLength(x, t.right, pl+1)
위에서 구현한 pathLength 함수를 이용하여 anomaly score를 계산할 수 있는 aScore 함수를 다음과 같이 구현한다.
def aScore(ifrst,
x : np.ndarray,
n : int):
"""
:param ifrst : 앞서 구현한 iforest 모델
:param x: anomaly score 계산이 필요한 데이터 x (1D array)
:param n: 입력받은 전체 데이터 사이즈 (전체 데이터의 수)
:return:
"""
hx = 0
for itr in ifrst:
hx += pathLength(x, itr, pl=0)
Ehx = hx/len(ifrst)
return -1*Ehx / c(n)
위 구현에서는 각 부분을 따로 볼 수 있도록 개별 구현하였으나, 사실 위 메서드와 변수들은 iForest라는 1개의 기능으로 묶여있는 것이기 때문에 다음과 같이 클래스로 구현하는 것이 사용하기에 편리하다고 판단하여 다음과 같이 전체를 구현하였다. (class로 묶는 과정에서 일부 코드가 약간 변형된 부분이 있음)
from tree.node import Multivariate as MultiNode
import numpy as np
class IForest:
def __init__(self,
x : np.ndarray,
n = 100,
s = 256):
"""
:param x: iForest를 생성할 입력 데이터, 2차원 배열 데이터
예) shape of x : N x D (N : 데이터의 수, M : 데이터의 차원)
:param n: 트리의 수 (논문 default = 100)
:param s: 샘플 사이즈의 크기 (sub sample size) (논문 default = 256)
:return: iForest
"""
# STEP1 : 입력받은 데이터에 대하여 iForest 모델을 생성한다.
self.dSize = x.shape[0]
self.ifrst = self.iForest(x, n, s)
def __call__(self,
x : np.ndarray):
"""
:param x: anomaly score를 계산하고자 하는 타겟 데이터
:return:
"""
if x.shape[0] == 1:
s = self.aScore(x, self.dSize)
else:
s = []
for subx in x:
s.append(self.aScore(subx, self.dSize))
return s
def iTree(self,
x : np.ndarray,
hl : int,
ch = 0):
"""
입력받은 데이터 x에 대하여, isolation tree를 생성한다.
:param x: 입력받은 2차원 배열 데이터
예) shape of x : N x D (N : 데이터의 수, M : 데이터의 차원)
:param ch: 현 노드의 높이 (current height)
:param hl: 트리의 높이 제한 (height limit)
:return: iTree
"""
# STEP 1: 단말 노드에 해당하는지 확인
"""
<단말 노드에 해당할 조건>
1) 입력받은 데이터의 수가 1개다.
2) 조건 1)을 만족하지는 않지만, 입력받은 데이터가 서로 모두 같다.
3) 해당 데이터의 높이가 트리의 높이 제한에 도달하였다.
"""
# 단말 노드에 해당하는 경우
if x.shape[0] == 1 or ch >= hl or (x[0]==x).all():
return MultiNode(value=x,
sDim=None,
sVal=None)
# 단말 노드에 해당하지 않는 경우
else:
sDim = np.random.choice(x.shape[1]) # 분할 차원 임의 선택
sVal = (np.max(x[:, sDim])-np.min(x[:, sDim]))*np.random.random() + np.min(x[:, sDim]) # 분할 값 임의 설정
mask = x[:,sDim] < sVal
return MultiNode(value=x,
sDim=sDim,
sVal=sVal,
left=self.iTree(x=x[mask], ch=ch+1, hl=hl),
right=self.iTree(x=x[~mask], ch=ch+1,hl=hl))
def iForest(self,
x : np.ndarray,
n : int,
s : int):
"""
입력받은 데이터 x에 대하여, iForest를 생성한다.
:param x: 입력받은 2차원 배열 데이터
예) x = N x D (N : 데이터의 수, M : 데이터의 차원)
:param n: 트리의 수
:param s: 샘플 사이즈의 크기 (sub sample size)
:return: iForest
"""
# initialize iForest
iForest = []
hl = np.ceil(np.log2(s)) # 트리의 높이 제한 (평균 높이로 제한)
for _ in range(n):
sub = np.random.choice(x.shape[0], s, replace=False) # 비복원추출
subTree = self.iTree(x=x[sub], hl=hl, ch=0)
iForest.append(subTree)
return iForest
def aScore(self,
x : np.ndarray,
n : int):
"""
:param x: anomaly score 계산이 필요한 데이터 x (1D array)
:param n: 입력받은 전체 데이터 사이즈 (전체 데이터의 수)
:return:
"""
hx = 0
for itr in self.ifrst:
hx += self.pathLength(x, itr, pl=0)
Ehx = hx/len(self.ifrst)
return -1*Ehx / self.c(n)
def pathLength(self,
x : np.ndarray,
t : MultiNode,
pl : int):
"""
:param x: path length를 계산할 데이터 x (shape of x : 1 x D)
:param t: iTree
:param pl: current path length
:return:
"""
# 단말 노드에 도달한 경우 (proper binary tree이므로, 한쪽이라도 자식이 없으면 단말노드다.)
if t.left is None:
return pl + self.c(t.Val.shape[0])
else:
if x[t.sDim] < t.sVal:
return self.pathLength(x, t.left, pl+1)
elif x[t.sDim] >= t.sVal:
return self.pathLength(x, t.right, pl+1)
def c(self, n):
"""
Unsuccessful search의 평균값
:param n: 노드의 수
:return:
"""
return 2.*(np.log(n-1) + np.euler_gamma) - 2*(n-1)/2.
최초 데이터를 입력 받았을 때, 입력받은 데이터를 기준으로 iForest 모델을 생성하기 위하여 __init__로 모델 생성 부분을 구현하였다. 이후 해당 모델을 가지고 있는 인스턴스 자체를 iforest 함수처럼 사용하기 위하여 __call__을 사용하였다. 따라서 최초 인스턴스 생성 후, 해당 인스턴스에 anomaly score를 계산하고 싶은 데이터를 넣으면 해당 입력값에 대한 anomaly score가 추출된다.
iForest의 구현 부분은 이걸로 마무리하고, 논문에서 진행한 실험 및 평가에 대하여 요약하겠다.
5. Empirical Evaluation
ORCA, LOF, RF 과의 성능 비교 부분 생략(5.1 Comparison with ORCA, LOF and Random Forest)
5.2 Efficiency Analysis
해당 실험에서는 샘플링(sub-sampling) 사이즈 $\Psi$가 이상탐지에 미치는 영향에 대하여 분석을 진행하였다. 결론적으로는 많은 양의 데이터를 iForest 모델 생성에 사용하는 것은 추천하지 않는다. 저자에 따르면 $\Psi = 128, 512$ 정도가 적당하다. (데이터의 특성에 따라 다름) 샘플 사이즈를 늘린다고 해서 iForest의 처리속도가 급격하게 증가하는 것은 아니나, 굳이 적은 양의 샘플만으로도 성능이 충분히 나오기 때문에 굳이 샘플 사이즈를 크게 증가시킬 필요는 없다고 주장한다.
5.3 High Dimensional Data
해당 실험에서는 고차원의 데이터를 입력으로 받았을 때, 이를 개선하기 위한 통계적 추출방법을 소개한다. 일반적으로 데이터의 차원이 높아지게 되면, 이상탐지 모델(외 다른 모델도)의 성능에는 지대한 장애가 발생하게 된다. 저자에 따르면 iForest도 이러한 '차원의 저주' 문제에서 자유롭지 못하다. 따라서 저자는 첨도(Kurtosis)를 활용하는 통계적 방법으로 데이터를 '요약'하는 방안을 제시하고 있다.
즉, 데이터의 모집단에서 샘플(sub-sample)을 추출하고, 해당 샘플 데이터의 각 단일 차원에서 첨도를 계산한다. 이렇게 계산된 각 차원(속성)별 첨도를 이용하여 ranking을 부여한 후, 이 랭킹에 따라 데이터의 부분공간(sub-space)를 만들고, 이렇게 차원이 축소된 데이터를 이용하여 iForest 모델을 생성하는 방식이다. 물론 부분공간의 크기가 원 속성차원에 가까울 수록 탐지 성능은 향상되었으나, 이런 방식으로 데이터를 축소하여 접근하는 것도 탐지 성능 측면에서 상당히 고무적이었다고 저자는 설명한다. (The result is promising and we show that the detection performance improves when the subspace size comes closed to the original number of attributes.)
5.4 Training using normal instances only (생략)
6. Discussion
iForest의 계산복잡도가 상수이기 때문에 샘플의 사이즈를 크게 높이더라도 다른 모델에 비해 효율적이라는 내용
7. Conclusion
본 논문은 일반적으로 정상치 프로필을 생성하고, 이를 바탕으로 이상치를 탐지하는 기존의 모델과는 근본적으로 다른 iForest라는 방법을 제안하고 있다. iForest는 '양적으로 적고, 다르다'는 이상치의 특성을 이용하여, iTree에서는 이상치를 루트 노드와 상대적으로 가까운 위치에 '고립시킨다.' 이러한 특성으로 인해 iForest에서는 적은 양의 데이터만으로도, 이상치를 찾아내는 효과적인 여러 부분모델(iTree)들을 생성할 수 있다. 또한 계산 복잡도 또한 상수이기 때문에 ORCA, LOF, RF와 같은 기존 방법들에 비해 매우 빠른 처리 속도를 보이고 있다.
'25.05.08.